Asymptotically accurate and geometric locking-free finite element implementation of a refined shell theory

We are pleased to announce that Prof. Dr. Le Khanh Chau and colleagues recently published their work titled "Asymptotically accurate and geometric locking-free finite element implementation of a refined shell theory" in the journal Computer Methods in Applied Mechanics and Engineering
Abstract:

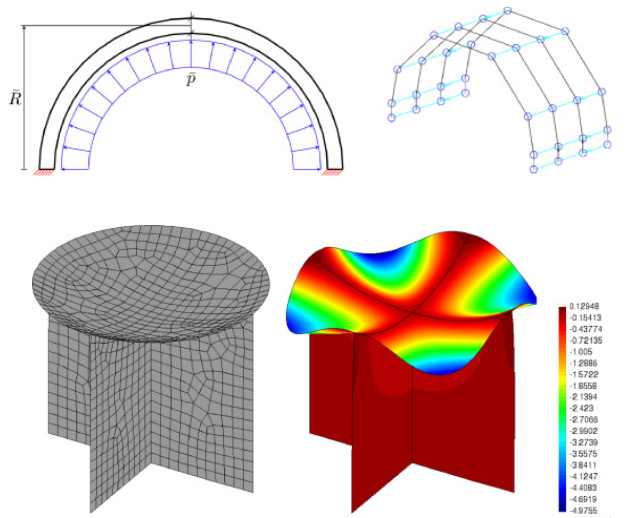
Accurate finite element analysis of refined shell theories is crucial but often hindered by membrane and shear locking effects. While various element-based locking-free techniques exist, this work addresses the problem at the theoretical level by utilizing results from asymptotic analysis. A formulation of a 2D refined shell theory incorporating transverse shear is developed using rescaled coordinates and angles of rotation, ensuring equal asymptotic orders of magnitude for extension, bending, and rotation measures and their respective stiffnesses. This novel approach, implemented via isogeometric analysis, is shown to be both asymptotically accurate relative to the underlying refined shell theory and inherently free from membrane and shear locking. Numerical simulations of semi-cylindrical shells show excellent agreement between the analytical solutions, 2D refined shell theory predictions, and 3D elasticity theory, validating the effectiveness and accuracy of the proposed formulation.